引言
方案是为了解决一个问题而存在的,因此所有的方案都有其原因,那我们今天的话题也不例外。
作为软件工程的一部分,计划在整个过程中占有举足轻重的地位,可以用一句官僚的话来说就是,它是一场战争的排头兵,直接影响了任务的成败。
当然我们没必要去评论这句话是不是有些夸大事实,但作为实务派的我们,这一点我们是切有体会的。
前述
读过《软件估算》这本书的朋友应该还记得这句话:估算和计划是两个相关的话题,但估算不是计划,计划也不是估算。估算应该看作是客观的(unbiased)分析过程;而计划应该看作是主观(biased)目标求解过程。
那么在这里,我们讨论的只是主观求解的若干想法,而其依据则是“估算”以及“经验”这两个数据来源(在《软件估算》一书中,“经验”也是估算的一种数据来源,《软件估算》.引言.P V)。
文中若干假设及数据大多来自此书,在此则不予以赘述。
6拍的故事
翻开《软件估算》的引言页,其楔子便是这个经典的“6拍”黑色幽默:在项目开始之前,你总是先“拍脑袋”得出进度和成本的承诺;在开工大会上领导“拍拍你肩膀”,是那样的语重心长、充满期待;而小酒刚下肚、春风正得意时,你不由得“拍胸脯”以表决心和能力;但在项目进展过程中遇到这样、那样的困难时,客户和业主不能不“拍桌子”了;这时充满悔意的你,只能“拍大腿”以示自责;而到了一切都覆水难收时,恐怕也只能“拍屁股”另谋高就了。(《软件估算》.引言.P III)
故事诚然是故事,此作也基于这个故事对客观数据进行了深入的归纳。但客观之于主观也仅仅是个皮球,事情常常陷入“数据你不妨估算,但脑袋我照样拍”的窘地。那么原因在哪里呢?对,就在这个“拍脑袋”之前的计划。
基础概念
在进入正文之前,我们有必要把几个基本概念澄清一下。
计划工作量
计划工作量即项目开始前,通过估算等手段对项目工作进行量化细分产生的成本。
计划工作重点考虑项目的设计以及创造性工作,可以由实际工作数据确定,具有计划性和高弹性。
预案工作量
为降低项目错误量、降低未知风险量而提前做出的预防性工作,由此产生的成本即为预案工作量。
对于软件项目,其主要体现在系统的规范性设计、标准化管理、防御性重构等工作上。其工作量会随项目的进程而减少。
风险工作量
风险即未知(未预期),风险工作量即为解决未知(未预期)原因造成的损害而产生的工作量。
对于创造性项目,该工作主要体现在解决已有错误和处理用户需求变动上。而对于不同级别的创造性项目,其风险的影响程度也不同,那么我们又可以引出“风险系数”的概念。
风险系数
对于创造性的项目,众所周知的是,错误的修正成本与系统规模成正比,而项目规模则与时间成正比,即,今天的工作与昨天(以及昨天的昨天)有关,错误修正越晚,修正成本越高,那么这一事实我们可以用一个简单的公式表示:
修正成本:f(t) = A·t·(t-1) ·(t-2)…(A为正常数,t为错误修正所推迟的时间)
同样,对于处理用户需求变动的工作量也有类似公式:
变更成本:f(t) = B·t·(t-1) ·(t-2)…(B为正常数,t为错误修正所推迟的时间)
那么对于整个开发工作的风险工作量可以用这样的函数来表示:
风险工作量:f(x) = xp (p>0)
其中x为项目规模(进度),p为风险带来的影响系数,即风险系数,其与项目的性质有关,与进度无关。该公式表示,风险系数越大,其风险工作量随项目规模增长所出现的增量越大。p>0说明了任何项目都会有风险。
一般模型
有一点值得我们欣慰的是,一般(或者是大多数的)管理人员都会在拍脑袋前对项目做一下总体的部署和分配。作为一个管理者,这个工作确实比拍脑袋要来的困难,但也并不是让人寝食难安的事情――或者这也是很多人都想做管理的原因。所以,业界通用的计划模型还不至于让这些管理者丢掉饭碗。
傻瓜式计划
恰恰是因为这些似乎是已成定式的工作方式,才导致了现在这种傻瓜式的计划:平均式计划模型。如下图所示。
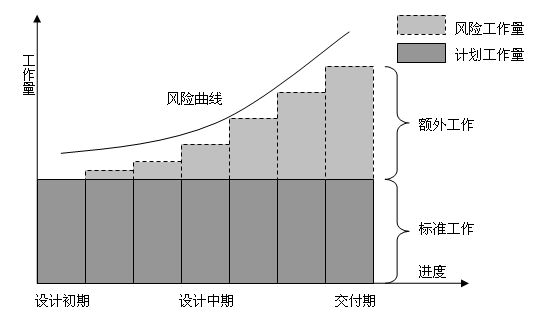
平均式计划模型
图中所示,实线部分是我们的管理者(或者计划部门)为开发人员(或者实施人员)制定的工作计划,一般可以认为是一个工作岗位能够承受的(人力或者资源成本)限度。而虚线部分则是在此计划之外出现的工作。那么两部分相加的和便是我们在单位时间内的工作量,我们可以看到它随着风险曲线的增长而增加。(具体的实况描述可以参阅我的另一篇拙作《今天还是明天――一个人的软件工程》)
两种结果
在这种计划模型下工作,一开始我们会感觉到事情很顺利,很轻松,而项目经理也可以胸有成竹的跟老板“拍胸脯”,但随着项目进程的不断推进,产出规模迅速增加,其缺陷、风险被成倍成十倍的放大之后,事先计划的工作量已经越来越不够用,那下面两种结果的出现应该是必然的了:
项目延期
持续加班
梯式模型
基于前述的平均式计划模型,我们可以基本确定,计划工作量平均分配会给后期工作带来较大困难――风险成本是无法避免的。
那么或许大家都已经想到了解决的办法――至少是一种想法――就是将工作量按实际需要而灵活分配,那么,这正是我们今天要讨论的话题,梯式模型。而针对不同的工作类型,我们有三种模型:被动梯式模型、主动梯式模型和混合梯式模型。
被动梯式模型
被动梯式模型主要是考虑了风险成本,而将计划工作量逐级提到设计初期,以便使项目后期余出充分的空间和资源来应对逐级增长的风险工作量,如下图所示。
被动梯式模型
从图中我们可以看到,随着项目进程的推进,标准工作量并没有发生变化,两种工作量之和满足标准工作的要求,资源能够被合理使用。
主动梯式模型
主动模型考虑了预案工作量能够化解未来风险的作用,在项目初期投入较大预案工作,并随着项目进程逐级减少,如下图所示。
主动梯式模型
该模型采用主动化解风险的方式,将未来可能被放大的风险工作量,提前到设计初期,消耗更少的成本进行解决,以降低项目进程中未知风险带来的影响,使之趋于水平。
从图中我们同样可以看到,随着项目进程的推进,标准工作量并没有发生变化,两种工作量之和满足标准工作的要求,资源能够被合理使用。
混合梯式模型
混合梯式模型则同时考虑了风险成本及预案成本,将风险工作量(逐级增加)和预案工作量(逐级减少)进行混合,使之形成相对平均的工作量之后,再与计划成本共同消耗标准工作。
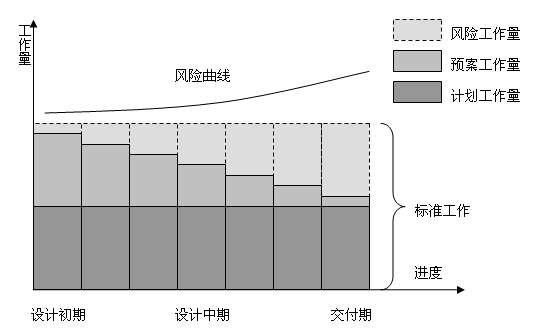
混合梯式模型
从图中可以看到,该模型吸取了被动和主动两种梯式模型的优点,使风险及预案进行合理互补,在保证标准工作进度的同时,将风险降低到项目可以接受的范围。
细心的你可能已经看到了一些端倪,的确,我们这个模型已经接近了目前流行的XP开发模式的工作模型:计划工作量只占标准工作的一部分,虽然存在风险,但另一部分的互补工作有效的化解了风险,保证了项目的质量和进度。
适用范围
前面我们讲到了“风险系数”这个概念,而在梯式模型中并没有使用到它,因为在我们的模型中无法量化的体现它的作用,在此单独释之。
两个极端
在前面的公式中,我们定义了p的概念,而且定义了p>0这个范围,而作为一个指数,0、1和大于1的数字,其函数模型并不相同,那我们来看这两个极端的情况:pà0和p>1。
当pà0的时候,我们的函数曲线是一个趋于水平的曲线(即无限趋近于水平线),这个时候我们可以说,风险不随或者几乎不随项目的进程而增加成本。
而当p>1的时候,我们得到的却是一个向上发散的无限增长曲线,风险几乎会在前一阶段的基础上增长另一个数量级。
在创造性项目中,确切的需求、规范的管理、良好的习惯都可以有效降低p值。
再释风险系数
前面我们说到,p风险系数是一个项目的固有性质,无法更改,其值也不可能小于等于0(任何项目都会有风险),因此我们的工作是怎样去在计划中,尽量使其对项目的影响降到最低。
基于不同的p值,我们可以选择不同的模型。
如果项目的p值较小(比如外包项目),则我们可以选择被动梯式模型,因为毕竟对于此类项目,需求较为明确,管理机制相对健全,过度的防御性工作则显得过于浪费。
如果项目的p值较大(比如需求不明的终端用户项目),我们可以选择主动梯式模型,因为对于需求不明确的项目,用户的需求存在较大变数,这对于项目的整体设计影响较大,因此应将防御性的预案工作提到首位,以最大程度降低项目的风险。
对于p值适中的项目,则可以考虑混合梯式模型。
结语
而今眼目下,对于成本和风险的控制,已经成为了每一个管理者甚至开发者关心的事情,甚至已经成为了这个时代的标志性语言――即便是拿这两个词来装点门面――但如火如荼的讨论却让人感觉到很少有人将其讨论到点上。或许是个人水平有限,无法参透那些高深莫测的符号曲线;也或许是人们习惯于只顾眼前而置将来于不顾。如果是前者,倒是比较让人放心,但诸多事实却一次次告诉我们,后者是对的。
计划对任何人都是一个考验,一个经验和魄力的考验,如此重要的一个环节,我们应该有充分的理由告诉自己在做什么,将要做什么。那么希望不才的一点点想法,能够让大家在探索之路上寻到些许的线索――哪怕是往深浅未测的河里扔下几块石头来垫脚。

